Research
As Common Core State Standards emphasize conceptual learning in mathematics instruction, so should elementary teachers. Esienhart, et al. (1993) asserts in a majority of schools, teachers allocate more time teaching procedural knowledge, specifically rote knowledge of rules and algorithms, compared to conceptually knowledge. Data from the fifth National Assessment of Educational Progress and the earlier Second International Mathematics Study indicate in the United States rote memorization governs mathematics instruction (Esienhart, et al., 1993). Hiebert and Wearne (1988) state students who make sense of mathematical procedures are an oddity. An example of this is when “students are expected to have speed and accuracy with simple calculations; teachers structure class time and/or homework time for students to memorize, through repetition, core functions such as multiplication tables so that they are more able to understand and manipulate more complex functions.” (Common Core Shifts, 2012, p.1). An obvious problem arises when mathematics instructional methodology is not aligned with state standards. This is not the teachers fault. Many teachers teach in regards to how they were taught. Conceptual knowledge has only recently become a priority in elementary mathematics education. Educational reform stresses the importance of training pre-service teachers to teach mathematics conceptually in order to align instruction with national goals and standards while improving an overall understanding of mathematics. Teaching students mathematical speed and memorization is a trend we as educators need to move away from (Boaler, 2015). It is important to question how teacher education programs will alter their curriculums in order to ensure the opportunity for pre-service teachers to teach and learn to teach for conceptual knowledge in response to educational reform. To effectively prevent the trend of elementary mathematics instruction being exclusively procedural, intervention and valuable teaching technologies should be present at the stage of pre-service teacher development.
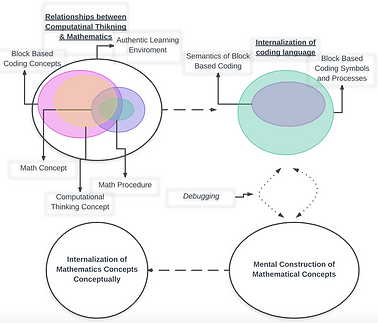
My research focuses on the motivation of elementary pre-service teachers to teach mathematics conceptually compared to procedurally in order to accurately align their instruction with state standards which place an emphasis on conceptual mathematics. Through the implementation of Scratch programing language into an elementary math curriculum, my hopes are teachers will be motivated to use this technology to effectively and engagingly teach mathematics conceptually. Coding language is like any other language consisting of symbols and rules to give an idea or concept meaning; computer programing is no different. "Scratching" is a programming term meaning to reuse existing code for a new purpose (Kte’pi, 2016). This is exactly what I would like to do with the Scratch programming language, also known as block-based coding, which has proved to be a motivating environment to explore mathematics and computer science concepts while increasing problem solving skills (Calder, 2010). An example of the direct relationship of computational thinking and mathematics concepts is using programming language to allow elementary students to internalize the concept of multiplication as repeated addition using the programming concept of “looping”. This is just one of many computational thinking and math concept correlations. By presenting teachers with implementation strategies for utilizing the Scratch program during instruction, they will hopefully feel more motivated to teach math conceptually. Gulbahar & Kalelioglu (2014) state that 5th grade students were more self-confident in their problem solving ability after using Scratch to learn computer science and they found the Scratch platform simple to use. My hopes are that elementary teachers also find this platform easy to use and eventually gain self-confidence in teaching math conceptually using block based programming. A professional development training module will need to be administered in order to motivate teachers and deliver content regarding instructional strategies. The research questions associated with the conceptual framework paper include:
- How can we motivate teachers to teach a content area they perceive themselves as weak in?
- Can the Scratch platform aid elementary teachers in teaching mathematics conceptually?
Conceptual Framework Diagram:
References:
Boaler, J. (2015). Fluency without fear: Research evidence on the best ways to learn math facts. Reflections, 40(2), 5–12.
Calder, N. (2010). Using Scratch: An integrated problem-solving approach to mathematical thinking. Australian Primary Mathematics Classroom, 15(4), 9–14.
Common Core Shifts. EngageNY. (2012). Retrieved March 25, 2017, from https://www.engageny.org/resource/common-core-shifts
Eisenhart, M., Borko, H., Underhill, R., Brown, C., Jones, D., & Agard, P. (1993). Conceptual knowledge falls through the cracks:
Complexities of learning to teach mathematics for understanding. Journal for Research in Mathematics Education, 24(1), 8.
https://doi.org/10.2307/749384
Gulbahar,Y., & Kalelioglu, F. (2014). The effects of teaching programming via Scratch on problem solving skills: A discussion from
learners’ perspective. Informatics in Education-An International Journal, 13(1), 33–50.
Hiebert, J., & Wearne, D. (1988). Instruction and cognitive change in mathematics. Educational Psychologist, 23(2), 105-117.
Kte’pi, B., MA. (2016). Scratch (programming language). Salem Press Encyclopedia of Science.